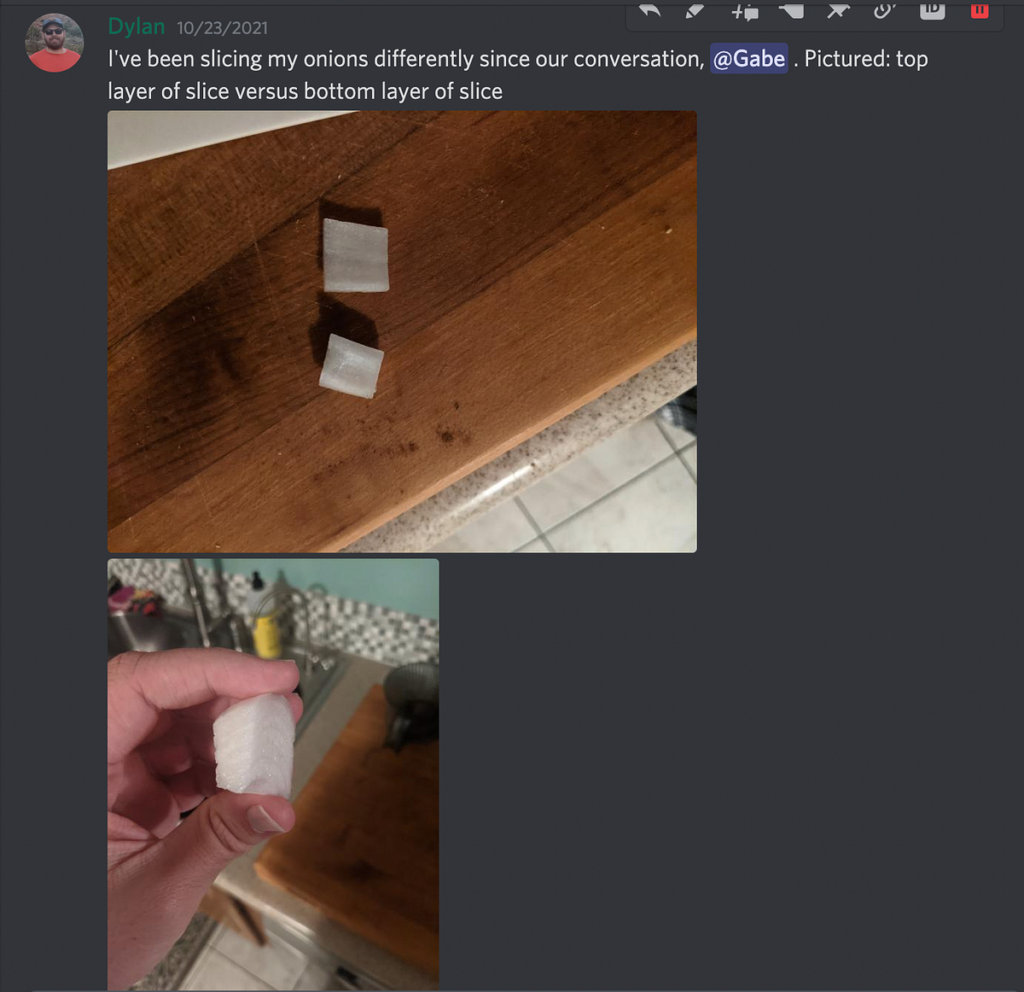
Here’s the technical part of the post. You probably need to know multivariable calculus to follow from here. I’m going to switch to using “we” instead of “I” to match mathematical writing conventions, and to indicate that we (you, dear reader, and I) are walking down this mathematical path together.

First, we model the onion as half of a disc of radius one, with its center at the origin and existing entirely in the first two quadrants in a rectangular (Cartesian) coordinate system. This ignores a dimension, and perhaps also some geometry of actual onions (are cross sections actually circles?) but makes the problem tractable and is still a good approximation.

The insight that leads to a solution comes from the Jacobian. When we change from rectangular coordinates to polar coordinates in integration, small rectangular pieces of area dx dy are transformed into small pieces of area r dr dθ, where x = r cos(θ) and y = r sin(θ). The idea of the Jacobian applies to all changes in coordinate systems. We can calculate the Jacobian as

Below is a diagram showing the change of coordinates and the Jacobian in this setting.

Notice that the coordinate system cuts the onion, much as usual grid lines cut the plane into rectangles in the Cartesian coordinate system. The radial part of the coordinate system cuts the onion radially (which of course nature does by default, but we need to model this mathematically), while the angular part of the coordinate system cuts the onion as our knife would if we were making straight cuts towards the center of the onion. Even though every piece of the onion is infinitely small (there are infinitely many layers, and infinitely many cuts) The Jacobian r dr dθ gives a measure of how big the infinitely small pieces are relative to each other. Pieces near the center of the onion are smaller than pieces near the edge of the onion, as we can see that since r is smaller towards the center of the onion and larger towards the edge of the onion.

We can find the average value of the function f(r,θ) = r over the part of the plane that defines the onion to find the average weight of the infinitesimal area, A.

Once we have the average, we can find the variance, v, of the weight of the infinitesimal area by calculating

The variance is a good measure of the uniformity of the pieces. If the variance is large, the pieces are not very uniform, and vice-versa.

The problem with this analysis, of course, is that we are cutting towards the center of the onion. We want to cut towards a point below the center of the onion. To accomplish this, we need a new coordinate system.

We make a coordinate system for cutting towards a point a distance h>0 below the center of the onion. In this coordinate system, we measure the angle theta from the point (0,-h), while we measure the radius from the origin (0,0) (both points in the rectangular coordinate system). The radial part of the coordinate system cuts the onion radially from the origin as before, while the angular part of the coordinate system cuts the onion as our knife would if we were making straight cuts towards the point (0,-h), below the onion.

This coordinate system only works for the upper half plane, as there are now technically two points in the plane for a given point (r,θ). Luckily, our onion is entirely in the upper-half plane!

In this coordinate system, the region of the plane that we model as the onion is defined by –arctan(1/h) ≤ θ ≤ arctan(1/h), and h |tan(θ)| ≤ r ≤1. We can eliminate the absolute value by using symmetry. Since the left side of the onion is a mirror image of the right side of the onion, and therefore both sides would have the same variance in area, we can perform this analysis just in the first quadrant. So, the region is defined by 0≤θ≤arctan(1/h), and h tan(θ) ≤r≤1.

The relation between (x,y) and (r,θ) is less clear. Given we know r, h, and θ, we can draw the following triangle, with a new variable c which represents the distance from the point (0,-h) to a given point (x,y) (both in the rectangular coordinate system).

First, using the law of cosines, we can calculate

Using this, we can find the relationship between (x,y) and (r,θ) as

From this, for a given depth h, we can calculate the Jacobian as

This is, to put it mildly, complicated. Nevertheless, we have done fairly straightforward calculus computations to get here, which shows the power of making this problem continuous. Mimicking what we did before, given a depth h, we can find the average weight of the infinitesimal area, A(h), by calculating the integral of the Jacobian over the onion region divided by the integral of 1 over the same region

And the variance of the weight of the infinitesimal area, v(h), is found by calculating the integral of the square of the Jacobian minus A(h) over the onion region divided by the integral of 1 over the same region

Yikes! Integrating this by hand looks really difficult, if not impossible. We should use a computer to help us. Using the power of numerical integration in Mathematica, we can plot the variance versus h, the depth of the point we are cutting towards.

We can see the minimum variance is around h=.55. We can use a numerical minimization technique to find the h that minimizes the variance.